arg ПП,-arg ПП1 = arg РР,-arg PPj,

н, следовательно,

Zn,nn,=:ZPiP,. (4)

Равенства (3) и (4) геометрически означают, что треугольники PiPP, и П1ПП2 подобны, так что бесконечно малый треугольник плоскости г отображается в подобный ему бесконечно малый треугольник плоскости С-Таким образом, рассматриваемое отображение сохраняет:

а) углы,

б) подобие соответствующих бесконечно малых треугольников. Благодаря этим свойствам отображение, определяемое формулой (1),

называют конформным отображением.

Соотношение (3) дает масштаб отображения в точке П. Этот масштаб является функцией z, т. е. изменяется от точки к точке. Иллюстрация конформного отображения дается обычной картой в проекции Меркатора. Хорошо известно, что угол между двумя линиями, измеренный на карте, равен углу пересечения двух соответствующих линий на земной поверхности; именно благодаря этому свойству карта полезна в навигации.

В частности, линии на карте, представляющие меридианы и параллели, перпендикулярны друг другу. Если мы рассмотрим малый участок карты, то установим, что расстояния, измеряемые на карте, представляют в измененном масштабе соответствующие расстояния на земном шаре, но этот масштаб изменяется с увеличением широты.

Из формулы (3) можно получить также отношение соответствующих величин малых площадей в следующем виде:

t = lfWI-rw7ff) = ff.

где 7(г) - комплексная сопряженная функция для функции /(z). Для иллюстрации последнего соотношения предположим, что

f(z)=6z-h3/z .

Тогда

/ (г) = 6 + 6/Z = 6 + 6t (дс -f- iy), 7(z) = 6-6/z = 6-6t (x-iy)

/(2)i = (6-6y) + (6x) .

5.71. Отображение бесконечных областей. В большинстве приложений конформного отображения к гидродинамике одна или обе рассматриваемые области простираются до бесконечности. Поэтому важно иметь ясное представление о том, что составляет внутреннюю часть области. Для объяснения этого рассмотрим отображение области плоскости z, ограниченной дугами окружностей г = а, г = Ь и радиусами 9 = 0, 9 = я/а (рис. 98), задаваемое функцией

C = z , а>1. Полагаем z = re*9, C = e v. Тогда

Таким образом, если точка г движется вдоль >4В(9 = 0), то у = 0 н точка С движется вдоль прямой А'В'. Если точка z движется вдоль CD (9 = я/а), то точка С движется вдоль СО.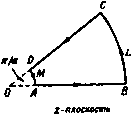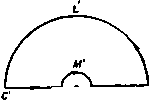

ff О'л'

-плоскость

Р и с. 98,

часть секторной области плоскости z конформно отображается на внутреннюю часть области, заключенную между полуокружностями в плоскости 1.

Кроме того, направление обхода сохраняется на обеих плоскостях, поэтому отображаемые области находятся слева, когда контуры обходятся в указанных направлениях. Эти утверждения остаются верными при любом увеличении величины b и, следовательно, полагая 6 со и отмечая точки в бесконечности индексами оо, мы получим области, изображенные на рис. 99, где штриховкой отмечены внешние области. Это показывает, что внутренняя часть бесконечной секторной области отображается на верхнюю половину плоскости С и теперь понятие внутренней части области означает предельную форму конечного

А CL D-0Л' е-

г-плоеяость -плосюстл

Рис. 99.

случая и таким же образом связывается, как и прежде, с направлением обхода. Выброшенная часть области в начале координат может быть теперь устранена, если величину а устремить к нулю.

Для уяснения смысла понятий внутренний и внешний при отображении бесконечных областей, вообще говоря, пригодны те простые соображения, которые указаны выше; действительно, уже одно знание направления обхода дает требуемые сведения.

ПРИМЕРЫ К ГЛАВЕ 5

1. Пусть ф-- ф = /(г) и пусть функция f (г) действительна при у = а. Показать, что ф = 0 при у = а.

2. Найти функцию комплексного переменного z, мнимая часть которой равна

2х (дг - Зу ) + у (х*-у*) + аху.

Если точка z движется вдоль дуги DMA (г = а), то точка С движется вдоль дуги О'М'Л'(/? = а ) и, наконец, если точка г движется вдоль дуги BLC{r = b), то точка I движется вдоль дуги BLC (R = b).

Ясно, что условия 5.62 (а) и (б) для отображающей функции выполняются, так как начало координат, в котором производная от функции обращается в нуль, исключена из рассматриваемой области. Таким образом, отображение является взаимно однозначным и непрерывным. Внутренняя

И

достигал минимума. Показать, что если ограничить ряд несколькими членами, то область В можно отобразить на почти круговую область.

12. Преобразование в примере 3 называется дробио-лииейиым преобразованием. Доказать, что обратное преобразование имеет вид г=( -б$--р)/(уС-а) и также является дробно-линейным преобразованием.

13. Пусть последовательные дробио-лииейиые преобразования преобразуют в Z и 1 в Z. Доказать, что преобразуется непосредственно в г с помощью дробно-линейного преобразования. Доказать, что все дробно-линейные преобразования образуют группу.

14. Доказать, что дробио-лииейиое преобразование отображает всю плоскость г (включая 2 =оо) саму на себя.

3. Пусть даны преобразования

(1) С = г+а. (II) С = ге* . (Ill) С = йг, (IV) С = г-1;

тогда доказать, что первое преобразование является переносом, второе -вращением, третье -вращением и растяжением, четвертое -инверсией относительно z = 1 и оси х (а-действительное число, величины а и 6 могут быть комплексными).

Доказать, что дробио-лииейиое преобразование 1=(аг-\-Р)/{уг-\-о), где аб-уфО, может быть составлено нз последовательного применения вышеуказанных преобразований и, следовательно, дает отображение, в котором окружности и прямые линии преобразуются в окружности и прямые линии.

4. Доказать, что преобразование С = (2- )/(гЧ-0 отображает верхнюю половину плоскости г на внутренность круга J = 1. Найти точки, соответствующие г = оо, -1,0, 1.

5. Доказать, что преобразование С = 2 отображает полуплоскость 9>0 на всю плоскость 5 с разрезом вдоль действительной полуоси.

е. В плоскости г дана область, ограниченная контуром, составленным нз окружности z = l и двух полуокружностей малого радиуса с центрами в точках z= ± 1; с помощью этих полуокружностей исключаются точки 2= i 1.

Доказать, что преобразование 5=-(- )/(+ ) отображает внутренность этой области на внутренность области, ограниченной полуокружностями малого и большого радиусов в верхней полуплоскости Z, с центрами в начале координат. Найти соотношение между радиусами полуокружностей в плоскости Z, и радиусом малой полуокружности в плоскости Z. Показать, что, когда последний стремится к нулю, рассматриваемая функция определяет отображение на всю верхнюю полуплоскость С-

7. Показать, что преобразование z=cosS отображает всю плоскость г с разрезом вдоль действительной оси от точки z= - оо до точки 2=1 на полубескоиечиый прямоугольник, ограниченный прямыми g=-я, =я, для которых г\> 0. Показать, что кривые = const являются софокусными эллипсами.

8. Показать, что функция

г= - 1п

я 1-е

отображает область, заключенную между прямыми у=а, у=-а, на внутреннюю часть круга единичного радиуса с центром в начале координат в плоскости 1,.

9. Пусть ОЛ-отрезок прямой y = xtg(kn), заключенный между точками х = 0 и x = /iCo.sfen, где <!< 1, и пусть ОВ-линия, соединяющая начало координат с точкой X--U- Показать, что преобразование

2=fe S-i (£- - )>+ (S-e*V~

отображает окружность единичного радиуса в плоскости С на ломаную линию АОВ, описываемую дважды, причем точки S = e , = е~* отображаются в начало координат, а точки S = e, J = e* ~P отображаются соответственно в точки А В, где sinp= = fesina, а f-подходящим образом выбранная константа.

10. Пусть круг I S К отображается на область В плоскости г посредством функции 2= J;--a2£*4-a3$-f ... . Доказать, что площадь В равна

я{ - +2а22г4+3аз2г +...}

и, следовательно, больше, чем п.пощадь данного круга.

11. Используя предыдущий пример, доказать, что задача отображения данной области В в плоскости S на круг в плоскости г сводится к задаче определения величии а;, аз, ... в разложении г= t-j-OoS-f-. . =/(С) таким образом, чтобы интеграл

отображает единичный круг г|<1 на единичный круг 5<1 и переводит точку г=с в точку S = 0.

17. Доказать, что преобразование

(г-Ц) -/(г-1) -(г4-1) -Ь.(г-1)*

отображает полукруг с диаметром, соединяющим точку г= -I и точку z=l, на единич-вый круг I СI < 1-

15. Доказать, что дробно-линейное преобразование

г-с

где с не является действительным числом, отображает полуплоскость (/>0 на единичный ФУГ 1С1<1 и отображает г = с иа J=0.

1в. Доказать, что дробио-лииейиое преобразование

S = e . с|<1 1-сг

Глава 6 ПОТЕНЦИАЛЬНЫЕ ТЕЧЕНИЯ

6.00, Комплексный потенциал. Пусть ф и ф -потенциал скорости и функция тока безвихревого двумерного движения невязкой жидкости. Приравнивая компоненты скорости, выран^енные через производные от потенциала скорости и функции тока, получим равенства

дур Ф

дх ду ду~ дх

Определим комплексный ттенциал движения жидкости соотношением

ш = ф -f- /ф.

Согласно п. 5.30, из равенств (1) следует, что потенциал w есть аналитическая функция комплексной переменной z = x + iy в любой области, в которой ф и ф являются однозначными функциями.

Обратно, если мы предполагаем, что w есть аналитическая функция переменной г, то действительная и мнимая части этой функции представляют собой потенциал скоростей и функцию тока для некоторого возможного двумерного безвихревого движения жидкости, так как они удовлетворяют уравнениям (I) и уравнению Лапласа.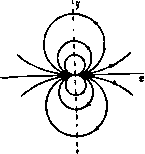

Рис. 100.

Р и с. 101.

Так, например, функция ш = г* характеризует движение жидкости с потенциалом скоростей ф = д: -у* и функцией тока ф = 2д:1/. Это движение уже было изучено в п. 4.70.

Так как iw также является функцией г, то, следовательно, - ф и ф являются потенциалом скоростей и функцией тока некоторого другого движения, в котором линии тока и линии равного потенциала поменялись ролями.

Ниже будет установлено, что математический анализ двумерного движения жидкости существенно упрощается, если ввести комплексный потенциал вместо двух функций ф и ф. Это упрощение подобно тому, которое имеет место при использовании одного векторного уравнения вместо трех уравнений относительно проекций векторов в декартовых координатах. В двумерном случае мы имеем дело с одним уравнением относительно

ISO Глава 6

функций, зависящих от переменной г, вместо двух уравнений относительно функций, зависящих от переменных хну.

Размерность комплексного потенциала равна произведению размерности скорости на размерность длины, т. е. L*7.

Проиллюстрируем сказанное несколькими примерами. Будем обозначать скорость через U, а длину через а, причем U и а-действительные величины.

(I) w = Uz.

Б этом случае ф = 6/у, движение является однородным потоком, направленным вдоль отрицательной оси х (рис. 100).

(11)

Г х*-у*

Линии тока ф = const представляют собой окружности, касающиеся оси X в начале координат (рис. 101). Это течение вызвано диполем, помещенным в начале координат (см. п. 8.23).

> (III) w-Ua(±f.

уу f ( Течение, описываемое этим потенаиалом,

у f ( представляет собой обтекание некоторого угла

-- а; линии тока течения асимптотически при-

-2- --- ближаются к сторонам угла (рис. 102). Част-

* ный случай такого течения прн а = я/2 был

Рис. 102. рассмотрен в п. 4.70.

С математической точки зрения комплексный потенциал в форме w = f(z) определяет конформное отображение плоскости z на плоскость w. При этом линии тока течения в плоскости z переходят в прямые ф = const, параллельные действительной оси плоскости w. Нахождение такого отображения является основным принципом решения задач гидродинамики методами теории функций комплексного переменного.

6.01. Комплексная скорость. Путем дифференцирования комплексного потенциала а; = (р-Ь{ф можно получить равенства

Лр , . дф dw dw дг dw

По определению, и= -dffldx, v = dldx, следовательно, имеет место равенство

v = u-iv=-. (1)

Комбинация u - iv, которую мы обозначим через v, называется комплексной скоростью. Заметим, что комплексная скорость находится непосредственно из комплексного потенциала по формуле (1). Вектор, изображающий комплексную скорость, является отражением вектора действительной скорости относительно прямой, проведенной через рассматриваемую точку параллельно оси X (рис. 103).

Очень важно отметить, что производная -dwidz дает u - iv = v, а-не u--io = t3. Если мы хотим получить выражение ы +ш, то мы должны везде изменить знак перед i, так что u+iv= -dw/dz, где через w обозначена

комплексно сопряженная функция переменной г. Так, если w=iz*, то мы должны взять ш= - z, изменяя везде знак перед i- Тогда v = u-iv = = -2*2, а v = u-riv = 2iz и любое из этих выражений дает нам и = 2у, v = 2x.

В качестве простого приложения рассмотрим однородный поток, изображенный на рис. 75. Мы имеем

- = Qcoso - /<?sin а = откуда получаем

w= - Qe-* z.

u-ta

Рис. 103.

6.02. Критические точки. В критической точке скорость равна нулю, следовательно, и комплексная скорость равна нулю. Отсюда следует, что критические точки находятся как корни уравнения

Например, если a>= Va , то критические точки задаются урав-

iL ,

z =0.

Так, если я < а, критическая точка находится в бесконечности. Если же я > а, то критическая точка расположена в начале координат (см. рис. 102).

6.03. Скорость. Для определения скорости жидкости мы имеем формулу

г = 1/ Ы + У =

Кроме того, скорость можно определить следующим образом: q*a + v = (u-iv) (и-f у) = =.

Чтобы проиллюстрировать сказанное, предположим^ что a = 2z-l-3<z*, тогда ш = 2г-3/? и 7 = (2 4-6tz)(2-6tz)=4-l-36zz-fl2i(z-z) = 4-b + 36(je* + y )-24y.

В этом течении имеется критическая точка, которая определяется как корень уравнения 2 + 6/z = 0. Отсюда находим, что г = ЦЪ, следовательно, координаты критической точки (О, Va)-

6.04. Уравнения линий тока. Здесь мы приведем экономный метод, посредством которого часто можно получить уравнения линий тока ф -const. Пусть

а; = ф4- ф.

Тогда ехр((р-Ь(ф) = ехрш. Это равенство может быть записано следующим образом:

cos ф -Ь ief sin ф = X -f iY,

где через X и К обозначены действительная и мнимая части выражения ехрш.

Таким образом. Х = еЧсо5ф, К = е 81пф.

Исключая ф, мы получаем

Y = Xig.

Таким образом, когда ф = const, мы можем записать, что ig = k, и можем выписать уравнения линий тока в виде

Y = kX.

Давая постоянной k различные значения, мы получаем уравнения различных линий тока. Линии тока, соответствующие k=0 и к=-т, т. е. ф = пя и ф = (2п+1) я/2, задаются уравнениями

К = 0 и Х = 0.

6.10. Течение через отверстие. Если w есть функция z, то и z является функцией W, и иногда бывает полезно воспользоваться этой формой связи между 2 и ш.

Пусть z = ccha , тогда

дс -1- /у = с ch ф cos ф -f ic sh ф sin ф,

ДC==CChфCOSф, у = С8Ьф81пф.

Исключив ф, мы получим уравнение

c*cos*tf c*sin*tf

из которого следует, что линии тока ф = const являются софокусными гиперболами, большие и малые полуоси которых равны соответственно ссозф и С51пф, а фокусы расположены в точках (с, 0) и ( - с, 0) (рис. 104).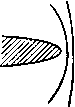

Рис. 104.

Если мы примем цилиндры, направляющими которых являются эти гиперболы, за фиксированную границу, то мы получим картину течения жидкости через отверстие, образованное этими цилиндрами. В предельном случае, взяв гиперболу, вырождающуюся в две прямые (ф = 0, я), мы получим течение через отверстие ширины 2с в плоской пластине. Однако этот предельный случай не соответствует физической картине течения, так как на краях отверстия скорость обращается в бесконечность.

Для доказательства этого мы используем следующее выражение для скорости:

=-4 = с*sh СС sh ш= -i-c [ch {w+w)- ch(w-w)]

-4-(ch 2ф-со8 2ф).

Ha краях отверстия в точках (с, 0) и ( - с, 0) мы имеем ф = 0, ф = 0 или ф = я. Таким образом, 1/9=0 и, следовательно, скорость обращается в бесконечность.

e.ll. Течение вокруг эллиптического цилиндра. Пусть дана функция 2 = ccosa , тогда.

Д: = ССЬфС05ф, у=-С5Ьф81Пф.

Исключив ф, придем к уравнению

c ch >> c sh t)

= 1.

из которого следует, что линии тока теперь являются софокусными эллипсами с полуосями ссЬф и с ship.

Если в качестве фиксированной границы мы примем цилиндр, направляющей которого является один из этих эллипсов, то получим течение

Рис. 105.

жидкости, вращающейся вокруг неподвижного цилиндра. В предельном случае, если положить ф=0, эллипс вырождается в отрезок длины 2с и мы получим течение жидкости, вращающейся вокруг плоской пластины длины 2 с (рис. 105). В этом случае скорость на концах пластины снова обращается в бесконечность, так как выражение

q* dw dw

обращается в нуль при г= ±с. Кроме того, когда величи на \г\ велика, мы можем приближенно записать, что q = \lr, где r=z=z.

Так как cosia = cha , то мы видим, что из формул этого и предыдущего пунктов следует, что линии тока и линии равного потенциала меняются ролями, если заменить w на iw (см. п. 6.00).

6.21. Теорема об окружности. Докажем теперь одну общую теорему'), которая будет нам весьма полезна в дальнейшем.

Теорема об окружности. Пусть в плоскости г имеется двумерное безвихревое течение несжимаемой невязкой жидкости. Пусть твердые границы отсутствуют и пусть комплексный потенциал этого течения задается функцией f(z), причем все особые точки функции / (г) удалены от начала координат на расстояние, большее чем а. Если в япо течение жидкости поместить цилиндр, образующей которого является окружность С : I г I = о, то комплексным потенциалом нового течения будет функция

=/(2)+f(4).

Доказательство. Так как г=а*/г*) на окружности С, то мы

) Milne-Thomson, Proc. СатЬ. Phil. Soc., 36 (1940).

) На окружности С: z-aeiO , г = ав~* г=-.- Прим ред.

видим, что функция W, определяемая равенством (1), является действительной на окружности С и, следовательно, ф=0. Таким образом, С есть линия тока.

Если точка z расположена вне окружности С, то точка а'/г расположена внутри нее, и наоборот. Так как все особые точки функции /(г) по предположению находятся вне окружности С, то все особые точки

функции 7 (aVz) расположены внутри С; в частности, функция / (aVz) не имеет особенности на бесконечности, так как функция /(z) не имеет осо-<Зенности в нуле. Таким образом, функция а; имеет те же особенности, что и функция f(z), и, следовательно, w является комплексным потенциалом нового течения.

6.22. Потенциальное обтекание кругового цилиндра. Рассмотрим течение с комплексным потенциалом Uz. Если мы поместим в это течение цилиндр \z\=a, то в силу теоремы об окружности комплексный потенциал нового течения будет иметь вид

ie=t/(z + 4)- (I)

Следовательно, функция w является комплексным потенциалом обтекания кругового цилиндра потоком жидкости, скорость на бесконечности которого равна и и направлена вдоль отрицательной оси х. Вообще, такое течение называют обтеканием цилиндра однородным потоком. Действительно, поток испытывает возмущение только из-за присутствия цилиндра и остается однородным на большом расстоянии от него. Введенный термин оказывается удобным для наглядного представления течения.

В более общем случае если мы поместим цилиндр в однородный поток с комплексным потенциалом t/6~ z, то в силу теоремы об окружности новое течение описывается комплексным потенциалом

a; = £/ze-< + - (2)

Если центр цилиндра находится в точке Zo, то с помощью простого переноса начала координат мы получим выражение для комплексного потенциала этого течения в виде

a; = f/ze-* + 7. (3)

Найдем уравнение линий тока течения, описываемого потенциалом (1). Так как z = re*, то

ф= f/(rsine-4 sin ®) =У(1 --7 ) =

где

Полагая ф| =/nt/a, фа = -nt/a, мы приходим к уравнениям

из которых следует, что линии тока, соответствующие функциям ф, и фа. являются прямыми, параллельными оси х, и окружностями, касающимися оси X в начале координат. Задавая параметрам тип значения 0,1, 0,2, 0,3, ..., с помощью метода Рэнкина можно построить картину линий тока (см. п. 4.32).