Тогда функция f{z), равная fi{z), если z находится в области Ri, и равная /2(2), если z находится в области R2, является аналитической функцией во всей области Ri-bRi- Для доказательства достаточно показать только, что выполнено равенство

f{z)dz = 0.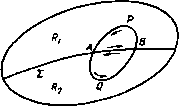

Рис. 89.

если С -некоторый контур внутри области --2- Так как fi{z), /2 (z) - аналитические функции в каждой из областей, то единственным случаем, для которого это не очевидно, является тот, при котором контур пересекает линию S (рис. 89). Для такого контура имеем

[f{z)dz= с h(z)dz+ 5 h(z)dzO,

(С) (аврл) (лова)

так как интегралы вдоль отрезков АВ и ВА взаимно уничтожаются. Таким образом, по теореме Морера функция / (z) является аналитической во всей области Ri + Ri-

В условиях данной теоремы обычно говорят, что функция /2 (г) есть аналитическое продолжение функции /1 (z) в области R2.

5.53. Принцип симметрии. Пусть /i (z) - аналитическая функция, определенная внутри области i, ограниченной прямой линией 2, на которой fi(z) принимает действительные значения.

Пусть i?2 -зеркальное отражение области Ri относительно линии S. Пусть точка Р2-отображение точки Pi относительно линии S.

Чтобы аналитически продолжить функцию /t(z) в область R2, нужно взять в качестве /2(2) функцию, значение которой в каждой точке Рг равно комплексно сопряженному значению функции fi(z) в соответствующей точке Pi (рис. 90).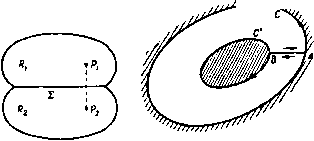

Рис. 90.

Рис. 91.

5.54. Деформация контура. Применим теорему Коши к контуру, состоящему из двух замкнутых кривых С, С и линии АВ, соединяющей две точки контуров, как показано на рис. 91.

Тогда, предполагая, что функция / (z) - аналитическая на кривых С и С и в каждой точке области, заключенной между ними, мы имеем

\ f{z)dz+ I f{z)dz- I f(z)dz+ I f{z)dz = 0.

{Alt)

(c )

(BA)

Интегралы вдоль АВ н ВА сокращаются, потому что f{z) однозначна, н, следовательно.

{ f{z)dz= I

(С) (С')

f{z)dz.

причем оба интеграла берутся по соответствующим контурам С и С в положительном (против часовой стрелки) направлении.

Это означает, что контур С можно заменить уменьшенным контуром С при условии, что / (z) остается аналитической в каждой точке между С и С. Точно так же контур С можно увеличить до контура С

5.55. Случай, когда функция не аналитнчна в некоторых точках.

Способ доказательства из п. 5.54 можно применить для получения весьма важного результата. Пусть функция аналитнчна в конечном числе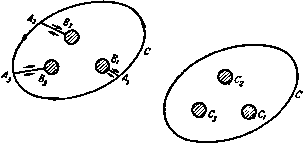

Р н с. 92.

точек внутри контура. В этом случае всегда можно провести окружности достаточно малого радиуса с центрами в этих точках, так чтобы каждая окружность содержала внутри себя только одну точку, в которой функция не аналитична. Мы можем соединить эти окружности непересекающимися прямыми линиями с контуром С. На рис. 92 показан случай, когда функция не аналитична в трех точках. Окружностями являются Ci, Сг, Сз; отрезками прямых линий AiBi, АгВг, АзВг эти окружности соединяются с контуром С. По интегральной теореме Коши имеем

(С) (AiBi) (Ci) (BiAi) (AjB,) (Ct) (BiAt) (AjBj) (Cg) (BjAj)

где повсюду подинтегральным выражением является f{z)dz. Таким образом, получаем

\ f{z)dz= [ f{z)dz+ \ fiz)dz+ 5 f{z)dz.

(С) (Ci) (Ct) (C )

Это означает, что интеграл по контуру можно заменить суммой интегралов по малым окружностям с центрами в точках внутри контура, в которых функция неаналитическая.

5.56. Особенности. Точка, в которой функция не является аналитической, называется особой точкой этой функции. Таким образом, функция f {z) = {z-a) аналитична в любой области, из которой исключена точка z = a (например, если провести около нее малую окружность). В точке z = а функция бесконечна и, следовательно, не удовлетворяет первой части определения аналитичности.

Если вблизи точки г = а функция может быть разложена в следующий ряд по положительным и отрицательным степеням г-а:

/ (г) = ... + ЛПг - а) +Л, (z - а) + Ло + ++ .

то точка 2 = 0 есть особая точка.

Если в этом разложении содержится только конечное число отрицательных степеней z-a, то точка 2 = а называется полюсом функции /(2).

Рассмотрим снова функцию /(2) = In 2. Эта функция не аналитична в точке 2=0. В п. 5.20 мы видели, что Inz-многозначная функция. Если мы сделаем эту функцию однозначной, положив lnz = 0 при z= 1, и заставим описывать замкнутую кривую, не окружающую точку z=0, то Inz возвратится к своему первоначальному значению и, следовательно, эта функция будет аналитической внутри кривой.

5.57. Вычеты. Мы видели, что функция, которая в окрестности г = а имеет разложение, содержащее отрицательные степени (z-a), имеет особенность в точке z = o.

В этом случае коэффициент при (z - a) называется вычетом функции при z = a.

Рассмотрим интеграл

5 (z-ardz.

взятый по окружности радиуса R с центром в точке г = о. На этой окружности z-a-=Re* и, следовательно,

J (2-a) dz= /? * в( +Яв,-9 = -1[е(п+1)!в)2я,= 0, о

если п Ф -

Однако если п = - 1, то мы получаем

Теперь предположим, что f (z) в окрестности точки г = а можно разложить в ряд

... +AAz-a)* + Ai iz-a) + Ao++j+ ....

Интегрируя этот ряд по малой окружности, окружающей точку z = a, получаем

5 /(z)dz= 2я А„

так как все интегралы, за исключением интеграла от члена fli(z -а) , обращаются в нули.

Таким образом, отсюда видно значение вычетов. Они образуют единственные вклады в интегралы от функции, являющейся аналитической во всех точках внутри замкнутого контура, за исключением особых точек описанного выше вида.

5.58. Теорема Коши о вычетах. Пусть С-замкнутый контур, внутри и вне которого функция / (г) аналитическая, за исключением конечного

f{z)dz=2ni(ai + at+...+an).

Доказательство. Предположим, что имеются три особые точки. Окружим их малыми окружностями, как описано в п. 5.55. Тогда, согласно п. 5.57, имеем

U{z)dz= I f{z)dz+ J f(z)d2+ I f(z)dz =

(C) (Ci) (C,) (C,)

= 2n/ai + 2niat + 2niO.

Это доказывает теорему в случае трех особых точек. Доказательство для любого конечного числа точек такое же.

5.59. Формула Коши. Пусть f (О-функция комплексного переменного S, аналитическая внутри и на замкнутом контуре С, и пусть z-какая-либо

точка, не лежащая на С. Тогда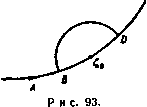

Ш^С=/(г)нлн О,

смотря по тому, будет ли z внутри или вне С.

Доказательство. Возьмем функцию i(C) = [/(C)-/(2)l/(C-2). Функция F(C) аналитична всюду внутри с, за исключением точки £ = 2, где она неопределенная. Но поскольку аналитнчна, то

UmF(£)=r(2).

Будем считать, следовательно, функцию F (J) равной / (г) прн J = 2.

Согласно этому определению, F(C) аналитнчна всюду внутри С, и,

следовательно, по теореме Коши, F(OdC = 0. Поэтому, согласно теореме

Коши о вычетах,

(С) (С) *

смотря пб тому, будет ли точка z внутри или вне С.

5.591. Главное значение интеграла. Пусть Со -точка на дуге А (которая может быть замкнутым контуром). Рассмотрим интеграл

f (Со) = Scarfs. (I)

где fiZ) задана, если I движется по А. Подинтегральное выражение при С = £о становится бесконечным, таким образом, интеграл не определен. Опишем окружность с центром бесконечно малого радиуса е так, чтобы окружность пересекала дугу А в двух точках, скажем В и D (рис. 93). Обозначим через а часть дуги внутри окружности, т. е, дугу BD, и обозначим через А -а остальную часть дуги А. Говорят, что интеграл (1)

числа особых точек внутри С. в которых вычеты равны Ои Ог, ..., Оп. Тогда

существует как главное значение в смысле Коши, если существует предел

Заметим, что если интеграл существует в обычном смысле, то ои существует также в смысле главного значения; обратное неверно.

В частности, рассмотрим d£/(C-Со), взятый вдоль замкнутого кон-тура С. Здесь имеем

lim \ p=limHn(C-Co)l(c-a) = limt(arg(£-Co)J(c-a) = /ff.

Следовательно, главное значение в смысле Коши равно

5.592. Формулы Племеля. Пусть Сд-заданная точка на простом замкнутом контуре С и пусть ф (С)-функция, заданная на С так, что интеграл

существует по крайней мере в смысле главного значения.

Если выбрать положительное направление обхода, то кривая разделит плоскость на две области: L слева и R справа (см. рис. 88).

Рассмотрим формулу

Фм- 1 е Ф )г-- f ФЮ-Ф(г) . , J f Ф(г)е

w-asi с=1ь = 25йД-с=7- +Ш]=Г-

Если г находится в области L, то мы будем писать Ф* (г) для значений Ф(г), определяемых по интегральной формуле Коши

Теперь пусть точка г, оставаясь все время внутри области L, стремится к Тогда

ф* (Со)=ш I Е^ rfc+Ф (С). (4)

Далее, если г находится в области R, то, по теореме Коши о вычетах, d/iZ - z) = 0 и, следовательно, из формулы (2) находим

Таким образом, если точка z, оставаясь в области R, стремится к Со то мы получим

но Глава 5

Вычитая (5) из (4), мы получаем первую формулу Племеля

Ф*(Со)-ф- о)=Ф(и (6)

складывая (4) с (5), получаем вторую формулу Племеля)

ФЧи + ф-(Со) = 5Д|й^ (7>

Если вместо замкнутого контура С задана открытая дуга А, то формула еще остается справедливой, так как мы можем замкнуть дугу, соединяя ее концы и полагая функцию ф(С) равной нулю на этой смыкающей части.

Одним из наиболее ценных следствий первой формулы Племеля является следующая теорема.

Теорема Племеля. Функциональное уравнение

ФЧ£о)-ф-(Со)=ф(£о) (8)

на дуге А имеет частное решение

<а)

Это - единственное решение, которое аналитична во всей плоскости^ за исключением дуги А, и которое в бесконечности стремится к нулю.

Из формулы (6) сразу же следует, что функция (9) является решением. Для доказательства единственности обозначим через {г} разность двух решений, удовлетворяющих этим условиям. Тогда посредством подходящего определения функции W {г) на дуге А (где она неопределенная) мы получаем, что W (г) аналитична во всей плоскости, включая бесконечность, и, следовательно, по теореме Лиувилля, сводится к постоянной величине, которая должна быть равна нулю, так как Ф(г) в бесконечности обращается в нуль.

5.60. Нули. Если аналитическая функция f{z) может быть выражена в форме f(z) = {z-Zo)g(z), где л - положительное целое число и g(z) не равно нулю при z = Zo, то говорят, что функция f(z) имеет нуль кратности л в точке z=Zo. Если л = 1, то Zg является простым нулем.

Так как

/ (Z) = л (г-г,) - g (2) -f (2-2о) g (z),

то f (z) будет иметь нуль кратности л-1 прн z=Zo. В случае простого нуля / (2о) ф 0.

Таким образом, если / (z) Ф О внутри данного контура, в котором / (z) аналитична, то / (z) может иметь внутри этого контура только простые нули.

Кроме того, поскольку аргумент произведения равен сумме аргументов (см. п. 5.13), можно записать соотношение

arg / (z) = arg (z-Zo) +arg g{z) = n arg (z-Zo) -\-argg (z).

При вычислении нулей функции / (z) удобно рассматривать нуль кратности л как л нулей, равных между собой.

1) Piemel j J.. Ein Erganzungssatz..., Monatshefie fur Math, and Phys., 19(1908), 205-210.

[Формулы (6) и (7) впервые были выведены Ю. В. Сохоцким (1873 г.). позже И. Племелем (1908 г.) и затем при более общих условиях И. И. Приваловым (1918 г.). В отечественной литературе эта формула известна как формула Сохоцкого.- Прим. перев.\

5.61. Принцип аргумента. Если С -простой замкнутый контур, на котором /(z) не имеет нулей и внутри которого и на котором функция /(г) аналитична, то число N нулей функции /(z) внутри контура определяется формулой

2nV = [arg/(z)l(c,.

где квадратная скобка в правой части означает увеличение arg/(г), когда z описывает один раз контур С в положительном направлении.

Доказательство. Для простоты предположим, что внутри области имеется два нуля, скажем z, и 22, кратности л, и Лг (рис. 94). Тогда

/(Z) = (z-Z,) i(z-z2) fi(2),

где g(z) не имеет нулей внутри С. Таким образом, согласно п. 5.60,

arg / (z) = л, arg (z - z,) + л, arg (z - z) -I- arg g (z).

Когда точка z описывает контур С один раз в по- Рис. 94.

ложительном направлении, то каждый из аргументов arg(z -Z,) и arg (z-Zj) увеличивается на 2я, в то время как argg(z) возвращается к своему первоначальному значению.

Следовательно,

larg / (z)I(C) = 2я (л -I- Я1) = 2nN,

Пусть, кроме того, / (z) имеет нуль, скажем Zj, на контуре С. Если точка Z описывает контур один раз в положительном направлении, то arg(z -z3) увеличивается. Это увеличение равно я, если z3 обыкновенная точка С (см. рис. 132); в общем случае оно равно углу между касательными в точке z3, если в этой точке имеются две различные касательные <см. рис. 133). Таким образом, в любом случае имеем

(аг0/(г))(с,>2яЛ^.

где Л^ -число нулей функции /(z) внутри контура С.

5.62. Отображение. Пусть /(z) -функция комплексного переменного 2 = x-\-iy, аналитическая внутри и на замкнутом контуре С в плоскости X, у, которую мы будем называть плоскостью z (рис. 95). Возьмем второе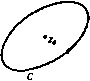

гплоскост

С-плоскость

Рис. 95.

комплексное переменное С = 5 + 1 и отметим изображающие точки на второй векторной диаграмме с осями 0% и Ог\. Эту плоскость мы назовем плоскостью Рассмотрим теперь соотношение

Ш Глава 5

Посредством этого соотношения каждой точке внутри контура С или на контуре соответствует одна точка в плоскости I, и поскольку f (г), будучи аналитической, однозначна, то точка является единственной. Таким образом, точки контура С и внутренняя область отображаются в некоторые точки плоскости С- Исследуем характер отображения при следующих допущениях:

а) функция /(г) никогда не принимает одинаковых значений в двух различных точках контура С;

б) производная / (г) не имеет нулей на контуре С.

Докажем теперь некоторые свойства отображения, задаваемого формулой (1).

(I) Если точка г описывает замкнутый контур С один раз, то точка £ описывает замкнутую кривую Г в плоскости и эта кривая не имеет двойных точек.

Доказательство. В силу аналитичности функции f (г) она изменяется непрерывно на контуре С, поэтому и величина С изменяется непрерывно, так что точка С описывает непрерывный контур Г.

В силу аналитичности функции f{z) она является однозначной функцией, поэтому, когда точка г описывает один раз контур С, возвращаясь к исходному положению, функция /(г) и, следовательно, величина £ возвращаются к первоначальному значению. Таким образом. Г -замкнутая кривая.

Согласно допущению (а), функция / (z) никогда не принимает одинакового значения дважды. Поэтому, когда точка z описывает контур С, то переменная величина С никогда не принимает одних и тех же значений дважды. Это означает, что кривая Г не пересекает сама себя, т. е. она не имеет двойных точек.

(II) Если внутри контура С дана точка Zg, то соответствующая точка находится внутри контура Г.

Доказательство. Пусть имеем

п = 2S (г) -/ (2о)}1(с) = (arg (£-Со)1(г).

Так как разность f(z) - f (zj имеет по крайней мере один нуль внутри контура С, а именно z то из п. 5.61 следует, что п>1.

Далее, когда точка описывает контур Г один раз, то увеличение arg (С -Со) равно О, ± а (где*) а< 2я) или ± 2я, смотря по тому, будет ли точка 1о вне, на или внутри контура Г.

Соответствующие значения п таковы: О, ± т, (т < 1), ± 1. Но п> 1. Отсюда л = 1 и, следовательно,

(arg(C-yj(r) = 2n.

Это показывает, что точка находится внутри контура Г и что контур Г описывается в положительном направлении. Это означает, согласно п. 5.40, что точка Со находится слева от наблюдателя, описывающего контур в положительном направлении.

(III) Если точка г описывает контур С в положите.чьном направлении, то точка С описывает контур Г тоже в положительном направлении.

Данная теорема является непосредственным следствием теоремы (II), согласно которой точка Со находится внутри контура Г и Г описывается в положительном направлении, если точка z описывает контур С в положительном направлении.

1) Кривая Г ие имеет двойной точки и, следовательно, а должно быть меньше 2л (см. рис. 132, 133).

(IV) Если внутри контура Г задана точка Со. существует только одна точка внутри контура С, такая, что Со = / (о)

Доказательство. Поскольку точка Со находится внутри контура Г, разность С -Со имеет только один нуль внутри Г, поэтому

1 = 2 (arg (С - Со)1(г) = i [arg {/ (г) - Со}](с,.

Отсюда следует, что разность /(z) -Со имеет только один нуль внутри контура С. Обозначая его через г^, получим /(z) -Со = 0.

(V) Производная /(z) не может обращаться в нуль внутри или на контуре С.

Доказательство. Допустим, что Zi является нулем функции /(г) внутри контура С. Тогда разность f(z) - f{Zi) имеет нуль кратности, большей 1, так как /(zi)=0 (п. 5.60).

Следовательно, уравнение f{z) - f{zi) = 0 имеет по крайней мере два корня в точке Zi, находящейся внутри С. Это противоречит теореме (IV) и, таким образом, предположение о том, что / (z) обращается в нуль внутри контура С, является ложным. То, что /(z) не может обратиться в нуль на контуре С, следует из допущения (б).

(VI). Если переменное С принимает значения внутри контура Г, то переменное г является аналитической функцией С.

Доказательство. Из теоремы (IV) следует, что каждому значению С внутри контура Г соответствует определенное значение г внутри контура С, так что z является однозначной функцией С-

Остается показать, что z имеет единственную конечную производную для каждого значения С внутри контура Г. Теперь если / (z) не равна нулю, то

dz Ydi\-i 1 dZ-\.dzJ -((z)

и так как значение f (г) единственно и не равно нулю, когда z двигается внутри контура С, то отсюда следует требуемый результат. В соответствии с допущением (б) результат остается верным, когда точка С движется по контуру Г.

Вышеуказанные результаты показывают, что соотношение (I) при выполнении допущения (а) дает взаимно однозначное и непрерывное отображение, при котором область, расположенная внутри контура С, точечно отображается на область, расположенную внутри контура Г, и обратно - внутренняя область контура Г точечно отображается на внутреннюю область контура С таким образом, что точке Zq внутри контура С соответствует одна и только одна точка Со внутри контура Г и, наоборот, точке Со внутри контура Г соответствует одна и только одна точка z внутри контура С. Добавление условия (б) обеспечивает то, что взаимно однозначный и непрерывный характер отображения распространяется на границы областей, контуры С и Г.

5.63. Контуры с нулями функции f{z). Предположим, что требуется отобразить контур С, на котором имеется нуль функции / (z), например, в точке Р.

Для осуществления этого отображения исключим эту точку контура С, т. е. заменим его видоизмененным контуром С, в котором бесконечно малая часть контура С, содержащего точку Р, выбрасывается и заменяется дугой окружности бесконечно малого радиуса с центром в точке Р, так что точка Р находится теперь вне видоизмененного контура С, как изображено на рис. 96.

Теперь к видоизмененному контуру С применяем теоремы об отображении. Затем полагаем, что радиус малой окружности стремится к нулю. На контуре по мере надобности могут быть сделаны такие операции во многих точках.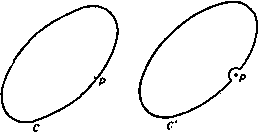

Р и с. 96.

5.70. Конформное отображение. Пусть взаимно однозначное и непрерывное отображение некоторой области плоскости z на область плоскости С определяется формулой

Пусть значения г, Zi, z, изображаются точками Р, Р Р, плоскости z и пусть соответствующие значения С, Ct. Cs представляются точками П, П III плоскости С (рис. 97). Тогда имеем

ii-if(h)-f(z) Сг-С f(z2)-Hz) 2i-2 гг-г г^-г

А

2 мосласт

П

с плоскость

Рис. 97.

Если предположить разности Zi-z и z-z малыми, то приближенно получим

77=/. -Г(г) (2)

и, следовательно,

г,-г г.-г dz

Zi-Z Zz-

Таким образом, приравнивая модули и аргументы обеих частей последнего равенства, находим соотношения

пп, ппг , . > I Ж arg ПП, - arg PPj = arg ПП, - arg РР = arg / (z).